3.9 Transformada integrales

Una transformada integral es cualquier transformada T aplicada sobre la funcion f(x) de la forma siguiente:

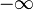La entrada de esta función T encontramos una función f(t), y la salida otra función F(u). Una transformada es un tipo especial de operador matematico. En ella t₁ y t₂ son dos valores que dependen de su definición, y pueden variar desde  hasta .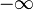

Hay numerosas transformadas integrales útiles. Cada una depende de la función K de dos variables escogida, llamada la función núcleo okernel de la transformación.

Algunos núcleos tienen una K inversa asociada, K ^{− 1}(u,t) , que (más o menos) da una transformada inversa:

Un nucleo simétrico es el que es inalterado cuando las dos variables son permutadas.

Ejemplo de uso

Como un ejemplo de un uso de las transformadas integrales, podemos considerar la transformada de laplace. Esto es una técnica que mapea ecuaciones diferenciales en el dominio del tiempo, en ecuaciones polinomiales en lo que es llamado el dominio de frecuencia compleja (La frecuencia compleja es similar a la frecuencia real, física, pero es más general. Expresamente, el componente imaginario ω de la frecuencia compleja s = -σ + iω corresponde al concepto habitual de velocidad angular, que se relaciona con la frecuencia por la identidadω = 2π f). Para su aplicación deben cumplirse ciertas condiciones en las funciones en que se aplicará, siendo la principal que estas deben cumplir con el principio de linealidad. Al trabajar con muchas transformadas, entre ellas la de Laplace, se facilitan los cálculos al contar con tablas para las transformaciones más comunes y sus propiedades.

Tabla de transformadasEn los límites de integración para la transformada inversa, c es un constante que depende de la naturaleza de la función transformada. Por ejemplo, para la transformaciones de Laplace simple y bilateral, c debe ser mayor que la parte real más grande de los ceros de la función transformada.

FUENTE:
http://es.wikipedia.org/wiki/Transformada_integral